¿Que es la Cinematica?
Cinemática
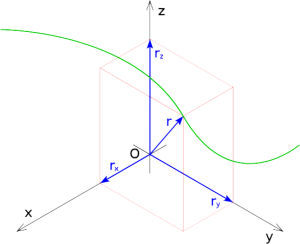
Represenación de la trayectoria de una partícula (verde), mostrando la posición (azul) en un momento dado de dicha trayectoria.
La cinemática (del griego κινέιν kinéin 'mover, desplazar') es la rama de la física que describe el movimiento de los objetos sólidos sin considerar las causas que lo originan (las fuerzas) y se limita, principalmente, al estudio de la trayectoria en función del tiempo. Para ello utiliza velocidades y aceleraciones, que describen cómo cambia la posición en función del tiempo. La velocidad se determina como el cociente entre el desplazamiento y el tiempo utilizado, mientras que la aceleración es el cociente entre el cambio de velocidad y el tiempo utilizado.
- 1Historia
- 2Terminología
- 3Elementos básicos de la cinemática
- 4Registro del movimiento
- 5Tipos de movimientos
- 6Formulación matemática con el cálculo diferencial
- 7Movimiento sobre la Tierra
- 8Cinemática relativista
- 9Véase también
- 10Referencias
- 11Bibliografía
- 12Enlaces externos
Historia
Los primeros en intentar describir el movimiento fueron los astrónomos y los filósofos griegos. Hacia 1605, Galileo Galilei hizo sus famosos estudios del movimiento de caída libre y de esferas en planos inclinados a fin de comprender aspectos del movimiento relevantes en su tiempo, como el movimiento de los planetas y de las balas de cañón.1 Posteriormente, el estudio de la cicloide realizado por Evangelista Torricelli fue configurando lo que se conocería como geometría del movimiento.
Luego, las aportaciones de Nicolás Copérnico, Tycho Brahe y Johannes Kepler expandieron los horizontes en la descripción del movimiento durante el siglo XVI. En 1687, con la publicación de los Principia, Isaac Newton hizo la mayor aportación conocida al estudio sistemático del movimiento. Entre otros numerosos aportes, estableció las tres leyes del movimiento que llevan su nombre, con lo que contribuyó al campo de la dinámica, además de postular la ley de gravitación universal.
El nacimiento de la cinemática moderna tiene lugar con la alocución de Pierre Varignon el 20 de enero de 1700, ante la Academia Real de las Ciencias de París.2 Fue allí cuando definió la noción de aceleración y mostró cómo es posible deducirla de la velocidad instantánea utilizando un simple procedimiento de cálculo diferencial.
En la segunda mitad del siglo XVIII se produjeron más contribuciones por Jean Le Rond d'Alembert, Leonhard Euler y André-Marie Ampère y continuaron con el enunciado de la ley fundamental del centro instantáneo de rotación en el movimiento plano, de Daniel Bernoulli.
Terminología
El vocablo cinemática fue creado por André-Marie Ampère, quien delimitó el contenido de esta disciplina y aclaró su posición dentro del campo de la mecánica. Desde entonces y hasta la actualidad la cinemática ha continuado su desarrollo hasta adquirir una estructura propia.
Con la teoría de la relatividad especial de Albert Einstein en 1905, se inició una nueva etapa, la cinemática relativista, donde el tiempo y el espacio no son absolutos, y sí lo es la velocidad de la luz.
Elementos básicos de la cinemática
Los elementos básicos de la cinemática son el espacio, el tiempo y un móvil.
En la mecánica clásica se admite la existencia de un espacio absoluto, es decir, un espacio anterior a todos los objetos materiales e independientes de la existencia de estos. Este espacio es el escenario donde ocurren todos los fenómenos físicos, y se supone que todas las leyes de la física se cumplen rigurosamente en todas las regiones del mismo. El espacio físico se representa en la mecánica clásica mediante un espacio euclidiano.
Análogamente, la mecánica clásica admite la existencia de un tiempo absoluto que transcurre del mismo modo en todas las regiones del Universo y que es independiente de la existencia de los objetos materiales y de la ocurrencia de los fenómenos físicos.
El móvil más simple que se puede considerar es el punto material o partícula; cuando en la cinemática se estudia este caso particular de móvil, se denomina Cinemática de la partícula, y cuando el móvil bajo estudio es un cuerpo rígido se lo puede considerar un sistema de partículas y hacer extensivos análogos conceptos; en este caso se le denomina cinemática del sólido rígido o del cuerpo rígido.
Fundamento de la cinemática clásica
La cinemática trata del estudio del movimiento de los cuerpos en general y, en particular, el caso simplificado del movimiento de un punto material, mas no estudia por qué se mueven los cuerpos sino que se limita a describir sus trayectorias y modo de reorientarse en su avance. Para sistemas de muchas partículas, por ejemplo los fluidos, las leyes de movimiento se estudian en la mecánica de fluidos.
El movimiento trazado por una partícula lo mide un observador respecto a un sistema de referencia. Desde el punto de vista matemático, la cinemática expresa cómo varían las coordenadas de posición de la partícula (o partículas) en función del tiempo. La función matemática que describe la trayectoria recorrida por el cuerpo (o partícula) depende de la velocidad (la rapidez con la que cambia de posición un móvil) y de la aceleración (variación de la velocidad respecto del tiempo).
El movimiento de una partícula (o cuerpo rígido) se puede describir según los valores de velocidad y aceleración, que son magnitudes vectoriales:
- Si la aceleración es nula, da lugar a un movimiento rectilíneo uniforme y la velocidad permanece constante a lo largo del tiempo.
- Si la aceleración es constante con igual dirección que la velocidad, da lugar al movimiento rectilíneo uniformemente acelerado y la velocidad variará a lo largo del tiempo.
- Si la aceleración es constante con dirección perpendicular a la velocidad, da lugar al movimiento circular uniforme, donde el módulo de la velocidad es constante, cambiando su dirección con el tiempo.
- Cuando la aceleración es constante y está en el mismo plano que la velocidad y la trayectoria, tiene lugar el movimiento parabólico, donde la componente de la velocidad en la dirección de la aceleración se comporta como un movimiento rectilíneo uniformemente acelerado, y la componente perpendicular se comporta como un movimiento rectilíneo uniforme, y se genera una trayectoria parabólica al componer ambas.
- Cuando la aceleración es constante pero no está en el mismo plano que la velocidad y la trayectoria, se observa el efecto de Coriolis.[cita requerida]
- En el movimiento armónico simple se tiene un movimiento periódico de vaivén, como el del péndulo, en el cual un cuerpo oscila a un lado y a otro desde la posición de equilibrio en una dirección determinada y en intervalos iguales de tiempo. La aceleración y la velocidad son funciones, en este caso, sinusoidales del tiempo.
Al considerar el movimiento de traslación de un cuerpo extenso, en el caso de ser un cuerpo rígido, conociendo como se mueve una de las partículas, se deduce como se mueven las demás. Más concretamente:
- En un movimiento plano bidimensional si se conoce el movimiento de 2 puntos del sólido, el movimiento de todo el sólido está determinado
- En un movimiento general tridimensional, el movimiento queda determinado si se conoce el movimiento de 4 puntos del sólido.
Así, considerando un punto del cuerpo, por ejemplo el centro de masa del cuerpo o cualquier otro, el movimiento de todo el cuerpo se puede expresar como:
{\displaystyle \mathbf {r} (t)=\mathbf {r} _{G}(t)+\mathbf {R} (t)\cdot (\mathbf {r} (0)-\mathbf {r} _{G}(0))}
donde:
-
{\displaystyle \mathbf {r} (t)}
, es la posición de un punto del cuerpo en el instante t.
-
{\displaystyle \mathbf {r} _{G}(t)}
, es la posición del punto de referencia (por ejemplo el centro de gravedad) en el instante t.
-
{\displaystyle \mathbf {R} (t)}
, es una matriz de rotación que da cuenta del giro del cuerpo alrededor de sí mismo en el instante t, para poder calcular esta matriz basta conocer la posición de otros 3 puntos además del punto de referencia (o 1 punto más si el movimiento es plano).
En la descripción del movimiento de rotación dado por
{\displaystyle \mathbf {R} (t)}
{\displaystyle \mathbf {R} (t)}
Un movimiento interesante es el de una peonza, que al girar puede tener un movimiento de precesión y de nutación. Cuando un cuerpo posee varios movimientos simultáneamente, como por ejemplo uno de traslación y otro de rotación, se puede estudiar cada uno por separado en el sistema de referencia que sea apropiado para cada uno, y luego, superponer los movimientos.
Sistemas de coordenadas
En el estudio del movimiento, los sistemas de coordenadas más útiles se encuentran viendo los límites de la trayectoria a recorrer o analizando el efecto geométrico de la aceleración que afecta al movimiento. Así, para describir el movimiento de un talón obligado a desplazarse a lo largo de un aro circular, la coordenada más útil sería el ángulo trazado sobre el aro. Del mismo modo, para describir el movimiento de una partícula sometida a la acción de una fuerza central, las coordenadas polares serían las más útiles.
En la gran mayoría de los casos, el estudio cinemático se hace sobre un sistema de coordenadas cartesianas, usando una, dos o tres dimensiones, según la trayectoria seguida por el cuerpo.
Registro del movimiento
La tecnología hoy en día nos ofrece muchas formas de registrar el movimiento efectuado por un cuerpo. Así, para medir la velocidad de los vehículos se dispone del radar de tráfico cuyo funcionamiento se basa en el efecto Doppler. El tacómetro es un indicador de la velocidad de un vehículo basado en la frecuencia de rotación de las ruedas. Los caminantes disponen de podómetros que detectan las vibraciones características del paso y, suponiendo una distancia media característica para cada paso, permiten calcular la distancia recorrida. El vídeo, unido al análisis informático de las imágenes, permite igualmente determinar la posición y la velocidad de los vehículos.
Tipos de movimientos
Movimiento rectilíneo
Es aquel en el que el móvil describe una trayectoria en línea recta.
Movimiento rectilíneo uniforme
En este movimiento el móvil se desplaza por una recta a velocidad: V constante, la aceleración:a es cero todo el tiempo. Esto corresponde al movimiento de un objeto lanzado en el espacio fuera de toda interacción, o al movimiento de un objeto que se desliza sin fricción. Siendo la velocidad V constante, la posición variará linealmente respecto del tiempo, según la ecuación:
-
{\displaystyle V={\text{constante}}\,}
-
{\displaystyle {\cfrac {d\,x}{d\,t}}=V}
-
{\displaystyle d\,x=V\;d\,t}
-
{\displaystyle \int _{x_{0}}^{x_{1}}d\,x=\int _{t_{0}}^{t_{1}}V\;d\,t}
-
{\displaystyle \int _{x_{0}}^{x_{1}}d\,x=V\;\int _{t_{0}}^{t_{1}}d\,t}
-
{\displaystyle x_{1}-x_{0}=V(t_{1}-t_{0})}
donde
{\displaystyle \ x_{0}}
{\displaystyle \ t_{0}}
Si
{\displaystyle \ x_{0}=0\;,\;t_{0}=0}
{\displaystyle \ x(t)=V\,t}
-
{\displaystyle x=V\;t}
Movimiento rectilíneo uniformemente acelerado
Figura 2. Variación en el tiempo de la posición, la velocidad y la aceleración en un movimiento rectilíneo uniformemente acelerado.
En este movimiento la aceleración es constante, por lo que la velocidad de móvil varía linealmente y la posición cuadráticamente con tiempo. Las ecuaciones que rigen este movimiento son las siguientes:
-
{\displaystyle a={\text{constante}}\,}
-
{\displaystyle {\cfrac {d\,V}{d\,t}}=a}
-
{\displaystyle d\,V=a\;d\,t}
-
{\displaystyle \int _{V_{0}}^{V_{1}}d\,V=\int _{t_{0}}^{t_{1}}a\;d\,t}
-
{\displaystyle \int _{V_{0}}^{V_{1}}d\,V=a\;\int _{t_{0}}^{t_{1}}d\,t}
-
{\displaystyle V_{1}-V_{0}=a(t_{1}-t_{0})}
-
{\displaystyle V_{1}=V_{0}+a(t_{1}-t_{0})}
la velocidad final es igual a la velocidad inicial del móvil mas la aceleración por el incremento de tiempo. si
{\displaystyle t_{0}=0}
-
{\displaystyle V=V_{0}+a\,t}
la velocidad final es igual a la velocidad inicial mas la aceleración por el tiempo.
Partiendo de la relación que calcula la velocidad:
-
{\displaystyle V=V_{0}+a\,t}
-
{\displaystyle {\cfrac {d\,r}{d\,t}}=V=V_{0}+a\,t}
-
{\displaystyle d\,r=(V_{0}+a\,t)\;d\,t}
-
{\displaystyle \int _{r_{0}}^{r_{1}}d\,r=\int _{t_{0}}^{t_{1}}(V_{0}+a\,t)\;d\,t}
-
{\displaystyle \int _{r_{0}}^{r_{1}}d\,r=V_{0}\int _{t_{0}}^{t_{1}}d\,t+a\int _{t_{0}}^{t_{1}}t\;d\,t}
-
{\displaystyle r_{1}-r_{0}=V_{0}(t_{1}-t_{0})+{\cfrac {1}{2}}a(t_{1}^{2}-t_{0}^{2})}
-
{\displaystyle r_{1}=r_{0}+V_{0}(t_{1}-t_{0})+{\cfrac {1}{2}}a(t_{1}^{2}-t_{0}^{2})}
Donde
{\displaystyle \ t_{0}=0}
{\displaystyle \ x_{1}}
{\displaystyle \ V_{0}}
{\displaystyle \ t=0}
-
{\displaystyle r=r_{0}+V_{0}t+{\cfrac {1}{2}}at^{2}}
Obsérvese que si la aceleración fuese nula, las ecuaciones anteriores corresponderían a las de un movimiento rectilíneo uniforme, es decir, con velocidad
{\displaystyle \ V=V_{0}}
{\displaystyle \ V_{0}=0}
Dos casos específicos de MRUA son la caída libre y el tiro vertical. La caída libre es el movimiento de un objeto que cae en dirección al centro de la Tierra con una aceleración equivalente a la aceleración de la gravedad (que en el caso del planeta Tierra al nivel del mar es de aproximadamente 9,8 m/s2). El tiro vertical, en cambio, corresponde al de un objeto arrojado en la dirección opuesta al centro de la tierra, ganando altura. En este caso la aceleración de la gravedad, provoca que el objeto vaya perdiendo velocidad, en lugar de ganarla, hasta llegar al estado de reposo; seguidamente, y a partir de allí, comienza un movimiento de caída libre con velocidad inicial nula.
Movimiento armónico simple[editar]
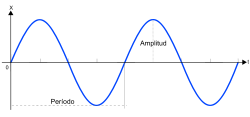
Es un movimiento periódico de vaivén, en el que un cuerpo oscila a un lado y a otro de una posición de equilibrio en una dirección determinada y en intervalos iguales de tiempo. Matemáticamente, la trayectoria recorrida se expresa en función del tiempo usando funciones trigonométricas, que son periódicas. Así por ejemplo, la ecuación de posición respecto del tiempo, para el caso de movimiento en una dimensión es:
{\displaystyle x(t)=A\sin \left(2\pi ft+\phi \right)}
ó
{\displaystyle x(t)=A\cos \left(2\pi ft+\phi \right)}
la que corresponde a una función sinusoidal de frecuencia
{\displaystyle f\,}
{\displaystyle \phi \,}
Los movimientos del péndulo, de una masa unida a un muelle o la vibración de los átomos en las redes cristalinas son de estas características.
La aceleración que experimenta el cuerpo es proporcional al desplazamiento del objeto y de dirección contraria, desde el punto de equilibrio. Matemáticamente:
{\displaystyle a={\frac {d^{2}x}{dt^{2}}}=-kx}
donde
{\displaystyle k\,}
{\displaystyle x\,}
La solución a esa ecuación diferencial lleva a funciones trigonométricas de la forma anterior. Lógicamente, un movimiento periódico oscilatorio real se ralentiza en el tiempo (por fricción mayormente), por lo que la expresión de la aceleración es más complicada, necesitando agregar nuevos términos relacionados con la fricción. Una buena aproximación a la realidad es el estudio del movimiento oscilatorio amortiguado.
Movimiento parabólico
El movimiento parabólico se puede analizar como la composición de dos movimientos rectilíneos distintos: uno horizontal (según el eje x) de velocidad constante y otro vertical (según eje y) uniformemente acelerado, con la aceleración gravitatoria; la composición de ambos da como resultado una trayectoria parabólica.
Claramente, la componente horizontal de la velocidad permanece invariable, pero la componente vertical y el ángulo θ cambian en el transcurso del movimiento.
En la figura 4 se observa que el vector velocidad inicial
{\displaystyle \ v_{0}}
{\displaystyle \ \theta _{0}}
{\displaystyle v_{0x}=v_{0}\cos \theta _{0}\ }
{\displaystyle v_{0y}=v_{0}\sin \theta _{0}\ }
El desplazamiento horizontal está dado por la ley del movimiento uniforme, por tanto sus ecuaciones serán (si se considera
{\displaystyle \ x_{0}=0}
{\displaystyle \ a_{x}=0}
{\displaystyle \ v_{x}=v_{0x}}
{\displaystyle \ x=v_{0x}t}
En tanto que el movimiento según el eje
{\displaystyle \ y}
{\displaystyle \ a_{y}=-g}
{\displaystyle \ v_{y}=v_{0y}-\ gt}
{\displaystyle \ y=y_{0}+v_{0y}t-{\frac {1}{2}}g{t^{2}}}
Si se reemplaza y opera para eliminar el tiempo, con las ecuaciones que dan las posiciones
{\displaystyle \ x}
{\displaystyle \ y}
{\displaystyle y=-{\frac {g}{2v_{0}^{2}\cos ^{2}{\theta _{0}}}}x^{2}+\tan \theta _{0}x+y_{0}}
que tiene la forma general
{\displaystyle \ y=a{x^{2}}+bx+c}
y representa una parábola en el plano y(x). En la figura 4 se muestra esta representación, pero en ella se ha considerado
{\displaystyle \ y_{0}=0}
{\displaystyle \ v_{y}}
{\displaystyle \ x}
{\displaystyle \ y=0}
{\displaystyle \ x}
Movimiento circular
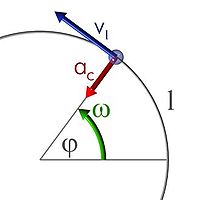
El movimiento circular en la práctica es un tipo muy común de movimiento: Lo experimentan, por ejemplo, las partículas de un disco que gira sobre su eje, las de una noria, las de las agujas de un reloj, las de las paletas de un ventilador, etc. Para el caso de un disco en rotación alrededor de un eje fijo, cualquiera de sus puntos describe trayectorias circulares, realizando un cierto número de vueltas durante determinado intervalo de tiempo. Para la descripción de este movimiento resulta conveniente referirse ángulos recorridos; ya que estos últimos son idénticos para todos los puntos del disco (referido a un mismo centro). La longitud del arco recorrido por un punto del disco depende de su posición y es igual al producto del ángulo recorrido por su distancia al eje o centro de giro. La velocidad angular (ω) se define como el desplazamiento angular respecto del tiempo, y se representa mediante un vector perpendicular al plano de rotación; su dirección se determina aplicando la "regla de la mano derecha" o del sacacorchos. La aceleración angular (α) resulta ser variación de velocidad angular respecto del tiempo, y se representa por un vector análogo al de la velocidad angular, pero puede o no tener la misma dirección (según acelere o retarde).
La velocidad (v) de una partícula es una magnitud vectorial cuyo módulo expresa la longitud del arco recorrido (espacio) por unidad de tiempo tiempo; dicho módulo también se denomina rapidez o celeridad. Se representa mediante un vector cuya dirección es tangente a la trayectoria circular y coincide con el del movimiento.
La aceleración (a) de una partícula es una magnitud vectorial que indica la rapidez con que cambia la velocidad respecto del tiempo; esto es, el cambio del vector velocidad por unidad de tiempo. La aceleración tiene generalmente dos componentes: la aceleración tangencial a la trayectoria y la aceleración normal a ésta. La aceleración tangencial es la que causa la variación del módulo de la velocidad (celeridad) respecto del tiempo, mientras que la aceleración normal es la responsable del cambio de dirección de la velocidad. Los módulos de ambas componentes de la aceleración dependen de la distancia a la que se encuentre la partícula respecto del eje de giro.
Movimiento circular uniforme
Se caracteriza por tener una velocidad variable o estructural constante por lo que la aceleración angular es nula. La velocidad lineal de la partícula no varía en módulo, pero sí en dirección. La aceleración tangencial es nula; pero existe aceleración centrípeta (la aceleración normal), que es causante del cambio de dirección.
Matemáticamente, la velocidad angular se expresa como:
{\displaystyle \ \omega =\omega _{0}={\text{const.}},\qquad \omega ={\frac {\Delta \varphi }{\Delta t}}}
donde
{\displaystyle \omega }
{\displaystyle \ \Delta \varphi }
{\displaystyle \ \Delta t}
{\displaystyle \ \varphi =\varphi _{0}+\omega t}
Movimiento circular uniformemente acelerado[editar]
En este movimiento, la velocidad angular varía linealmente respecto del tiempo, por estar sometido el móvil a una aceleración angular constante. Las ecuaciones de movimiento son análogas a las del rectilíneo uniformemente acelerado, pero usando ángulos en vez de distancias:
{\displaystyle \ \alpha =\alpha _{0}={\text{const.}}}
{\displaystyle \ \omega =\omega _{0}+\alpha t}
{\displaystyle \ \varphi =\varphi _{0}+\omega _{0}t+{\frac {1}{2}}\alpha t^{2}}
siendo
{\displaystyle \alpha \,}
Movimiento armónico complejo
Es un tipo de movimiento bidimensional o tridimensional que puede construir como combinación de movimientos armónicos simples en direcciones diferentes. Cuando una estructura se ve sometida a vibraciones el movimiento de un punto material concreto frecuentemente puede modelizarse por un movimiento armónico complejo si la amplitud del movimiento es pequeña.
El movimiento armónico complejo es interesante porque usualmente no es un movimiento periódico sino un movimiento cuasiperiódico que nunca se repite exactamente igual, aunque ejecuta casi ciclos sin repetirse exactamente. La forma vectorial de un punto que ejecuta este movimiento resulta ser:
{\displaystyle \mathbf {r} (t)=A_{x}\cos(\omega _{x}t+\phi _{x})\mathbf {i} +A_{y}\cos(\omega _{y}t+\phi _{y})\mathbf {j} +A_{z}\cos(\omega _{z}t+\phi _{z})\mathbf {k} }
donde
{\displaystyle A_{x},A_{y},A_{z}}
{\displaystyle \omega _{x},\omega _{y},\omega _{z}}
{\displaystyle \phi _{x},\phi _{y},\phi _{z}}
El movimiento circular uniforme de hecho es un caso de movimiento armónico complejo en el que las amplitudes en dos direcciones son iguales al radio del círculo
{\displaystyle (A_{x}=A_{y}=R,A_{z}=0)}
{\displaystyle (\omega _{x}=\omega _{y}=\omega )}
{\displaystyle (\phi _{x}=\phi _{y}\pm \pi /2)}
Movimiento de sólido rígido
Todos los movimientos descritos anteriormente se refieren a puntos materiales concretos, o corpúsculos, es decir cuerpos físicos cuyas dimensiones pequeñas respecto al tamaño de la trayectoria por lo que pueden aproximarse por puntos materiales. Sin embargo, los cuerpos físicos macroscópicos no son puntuales, en muchas situaciones el movimiento del cuerpo como un todo, requiere una descripción más compleja que la de asumir que todos sus puntos siguen una trayectoria mucho mayor que las distancias entre puntos del cuerpo, por lo que la descripción del cuerpo como punto material es inadecuada y la cinemática del punto material es demasiado simple para describir adecuadamente la cinemática del cuerpo. En esos casos debe emplearse la cinemática del sólido rígido, en la que la "trayetoria" del cuerpo se da un espacio más complejo o rico que el simple espacio euclídeo tridimensional, ya que se requiere definir no sólo el desplazamiento del cuerpo a través de dicho espacio, sino especificar las cambios de orientación del cuerpo en su movimiento, mediante movimientos de rotación.
Formulación matemática con el cálculo diferencial
La velocidad es la derivada temporal del vector de posición y la aceleración es la derivada temporal de la velocidad:
{\displaystyle \mathbf {v} ={\frac {d\mathbf {x} (t)}{dt}}=\mathbf {\dot {x}} ,\qquad \qquad \mathbf {a} ={\frac {d\mathbf {v} (t)}{dt}}={\frac {d^{2}\mathbf {x} (t)}{dt^{2}}}=\mathbf {\dot {v}} =\mathbf {\ddot {x}} }
o bien sus expresiones integrales:
{\displaystyle \mathbf {v} (t)=\mathbf {v} _{0}+\int _{0}^{t}\mathbf {a} (t)dt,\qquad \qquad \mathbf {x} (t)=\mathbf {x} _{0}+\int _{0}^{t}\mathbf {v} (t)dt=\mathbf {x} _{0}+\mathbf {v} _{0}t+\int _{0}^{t}(t-\tau )\mathbf {a} (\tau )d\tau }
donde
{\displaystyle \mathbf {x} _{0},\mathbf {v} _{0}}
Movimiento sobre la Tierra
Al observar el movimiento sobre la Tierra de cuerpos tales como masas de aire en meteorología o de proyectiles, se encuentran unas desviaciones provocadas por el llamado Efecto Coriolis. Ellas son usadas para probar que la Tierra está rotando sobre su eje. Desde el punto de vista cinemático es interesante explicar lo que ocurre al considerar la trayectoria observada desde un sistema de referencia que está en rotación, la Tierra.
Supongamos que un cañón situado en el ecuador lanza un proyectil hacia el norte a lo largo de un meridiano. Un observador situado al norte sobre el meridiano observa que el proyectil cae al este de lo predicho, desviándose a la derecha de la trayectoria. De forma análoga, si el proyectil se hubiera disparado a lo largo del meridiano hacia el sur, el proyectil también se habría desviado hacia el este, en este caso hacia la izquierda de la trayectoria seguida. La explicación de esta "desviación", provocada por el Efecto Coriolis, es debida a la rotación de la Tierra. El proyectil tiene una velocidad con tres componentes: las dos que afectan al tiro parabólico, hacia el norte (o el sur) y hacia arriba, respectivamente, más una tercera componente perpendicular a las anteriores debida a que el proyectil, antes de salir del cañón, tiene una velocidad igual a la velocidad de rotación de la Tierra en el ecuador. Esta última componente de velocidad es la causante de la desviación observada pues si bien la velocidad angular de rotación de la Tierra es constante sobre toda su superficie, no lo es la velocidad lineal de rotación, la cual es máxima en el ecuador y nula en el centro de los polos. Así, el proyectil conforme avanza hacia el norte (o el sur), se mueve más rápido hacia el este que la superficie de la Tierra, por lo que se observa la desviación mencionada. Lógicamente, si la Tierra no estuviese rotando sobre sí misma, no se daría esta desviación.
Otro caso interesante de movimiento sobre la Tierra es el del péndulo de Foucault. El plano de oscilación del péndulo no permanece fijo, sino que lo observamos girar, girando en sentido horario en el hemisferio norte y en sentido antihorario en el hemisferio sur. Si el péndulo se pone a oscilar en el ecuador, el plano de oscilación no cambia. En cambio, en los polos, el giro del plano de oscilación toma un día. Para latitudes intermedias toma valores mayores, dependiendo de la latitud. La explicación de tal giro se basa en los mismos principios hechos anteriormente para el proyectil de artillería.
Cinemática relativista
En la relatividad, lo que es absoluto es la velocidad de la luz en el vacío, no el espacio o el tiempo. Todo observador en un sistema de referencia inercial, no importa su velocidad relativa, va a medir la misma velocidad para la luz que otro observador en otro sistema. Esto no es posible desde el punto de vista clásico. Las transformaciones de movimiento entre dos sistemas de referencia deben tener en cuenta este hecho, de lo que surgieron las transformaciones de Lorentz. En ellas se ve que las dimensiones espaciales y el tiempo están relacionadas, por lo que en relatividad es normal hablar del espacio-tiempo y de un espacio cuatridimensional.
Hay muchas evidencias experimentales de los efectos relativistas. Por ejemplo, el tiempo medido en un laboratorio para la desintegración de una partícula que ha sido generada con una velocidad próxima a la de la luz es superior al de desintegración medido cuando la partícula se genera en reposo respecto al laboratorio. Esto se explica por la dilatación temporal relativista que ocurre en el primer caso.
La Cinemática es un caso especial de geometría diferencial de curvas, en el que todas las curvas se parametrizan de la misma forma: con el tiempo. Para el caso relativista, el tiempo coordenado es una medida relativa para cada observador, por tanto se requiere el uso de algún tipo de medida invariante como el intervalo relativista o equivalentemente para partículas con masa el tiempo propio. La relación entre el tiempo coordenado de un observador y el tiempo propio viene dado por el factor de Lorentz.3
Véase también
Cinematografia
-
Cine
(Redirigido desde «Cinematografia»)Caballo en movimiento (Animal locomotion) es una secuencia animada de un caballo de carreras galopando. Las fotos fueron realizadas por Eadweard Muybridge y se publicaron por primera vez en 1887 en Filadelfia.
El cine (abreviatura de cinematógrafo o cinematografía) es la técnica y arte de proyectar fotogramas de forma rápida y sucesiva para crear la impresión de movimiento, mostrando algún video (o de película, o film, o filme). La palabra «cine» designa también a las salas de cine o salas de proyecciones en las cuales se proyectan las películas.
Etimológicamente, la palabra «cinematografía» fue un neologismo creado a finales del siglo XIX y compuesto a partir de dos palabras griegas: por un lado κινή (kiné), que significa «movimiento» (ver, entre otras, «cinético», «cinética», «kinesis», «cineteca»); y por otro γραφóς (grafós). Con ello se intentaba definir el concepto de «imagen en movimiento».
Como forma de narrar historias o acontecimientos, el cine es un arte, y comúnmente, considerando las cincuenta artes del mundo clásico, se le denomina séptimo arte. No obstante, debido a la diversidad de películas y a la libertad de creación, es difícil definir lo que es el cine hoy. Sin embargo, las creaciones televisivas que se ocupan de la narrativa, montaje, guionismo, y que en la mayoría de los casos consideran al director como el verdadero autor, son consideradas manifestaciones artísticas, o cine arte (cine de arte). Por otra parte, a la creación documental o periodística se la clasifica según su género. A pesar de esto, y por la participación en documentales y filmes periodísticos de personal con visión propia, única y posiblemente artística (directores, fotógrafos y camarógrafos, entre otros), es muy difícil delimitar la calidad artística de una producción cinematográfica.
La industria cinematográfica se ha convertido en un negocio importante en lugares como Hollywood (California, Estados Unidos) y Bombay (la India), informalmente «Bollywood».
Historia[editar]
La historia del cine comenzó el 28 de diciembre de 1895, cuando los hermanos Lumière proyectaron públicamente la salida de obreros de una fábrica francesa en Lyon, la demolición de un muro, la llegada de un tren y un barco saliendo del puerto.1
El éxito de este invento fue inmediato, no solo en Francia, sino también en toda Europa y América del Norte, donde Thomas Edison ya había grabado numerosas escenas que un espectador a la vez podía ver a través de un kinetoscopio.
En un año, los hermanos Lumière crearon más de 10 películas, marcadas por la ausencia de actores y los decorados naturales, la brevedad, la ausencia de montaje y la posición fija de la cámara. Sin embargo, fue George Méliès quien inventó el espectáculo cinematográfico, en contraste con el tono documental de los Lumière. Con historias y decorados fantásticos, como "Fausto" y "Barba Azul" (1901), desarrolló las nuevas técnicas cinematográficas, sobre todo con Viaje a la luna (1902) y con Viaje a través de lo imposible (1904), aplicando la técnica teatral ante la cámara y creando los primeros efectos especiales y la ciencia-ficción filmada.
A partir de entonces, la cinematografía no hizo más que mejorar y surgieron grandes directores como Murnau, Erich von Stroheim y Charles Chaplin. En Estados Unidos se hicieron películas de aventuras, como las de Douglas Fairbanks y dramas románticos como las de Valentino. Sin embargo, las de mayor belleza fueron fruto de la escuela cómica americana nacida a partir de la comedia de Mack Sennett, basada en slapsticks y en la estereotipación de figuras sociales como el policía o el gordo, el avaro y el bigotudo burgués.
Aquí recordemos especialmente a Buster Keaton y a Charles Chaplin. En 1927, se estrenó la primera película con sonido El cantante de jazz, a partir de la cual el cine tal y como se conocía dejó de existir y de un lenguaje en que primaba la expresividad de segmentos que se contrastaban y juntaban se impuso una mayor continuidad del relato y mayor fluidez argumental. Ese mismo año apareció el doblaje.
En 1935 se filmó en Technicolor La feria de la vanidad (Becky Sharp), de Rouben Mamoulian; aunque artísticamente el color consiguió su máxima plenitud con Lo que el viento se llevó (1939).
La primera proyección pública de cine digital en Europa se realizó en París,2 el 2 de febrero de 2000, utilizando MEMS (DLP (Procesado digital de luz) CINEMA) desarrollado por Texas Instruments.3
Realización cinematográfica
La realización, en el ámbito audiovisual, es el proceso por el cual se crea un vídeo. Usualmente, en el cine de producción industrial pueden distinguirse cinco etapas de realización: desarrollo, preproducción, rodaje, postproducción y distribución. La realización supone asumir decisiones tanto a nivel artístico como productivo, y la limitación únicamente está dada por los medios disponibles (presupuesto del que se dispone y equipo con que se cuenta).
El equipo técnico está formado por:
Producción: El productor cinematográfico es el encargado de los aspectos organizativos y técnicos de la elaboración de una película, se podría decir que es el responsable de convertir la idea en película. Está a cargo de la contratación del personal, del financiamiento de los trabajos y del contacto con los distribuidores para la difusión de la obra. Si su tarea se limita a algunos aspectos puntuales del proceso técnico o creativo, se lo llama "co-productor".
También forman parte del área el director de producción, el productor ejecutivo, el jefe de locaciones y el asistente de producción.
Dirección: El director cinematográfico es el profesional que dirige la filmación de una película, el responsable de la puesta en escena, dando pautas a los actores y al equipo técnico, tomando todas las decisiones creativas, siguiendo su estilo o visión particular, supervisando el decorado y el vestuario, y todas las demás funciones necesarias para llevar a buen término el rodaje.
También forman parte del área el asistente de dirección y el denominado script o continuista. Por otro lado, trabaja en conjunto con el director de actores.
Guion: El guionista es la persona encargada de confeccionar el guion, ya sea una historia original, una adaptación de un guion precedente o de otra obra literaria. Muchos escritores se han convertido en guionistas de sus propias obras literarias. Dentro del guion cinematográfico se distinguen el guion literario o cinematográfico, que narra la película en términos de imagen (descripciones) y sonido (efectos y diálogo), y está dividido en actos y escenas. Es necesario distinguir el guion literario del guion técnico, que agrega al anterior una serie de indicaciones técnicas (tamaño de plano, movimientos de cámara, etc.) que sirven al equipo técnico en su labor y que, a diferencia del guion literario, suele elaborarlo el director, no el guionista.
También pueden colaborar con el guionista otros escritores (coguionistas) o contar con dialoguistas que están especializados en escribir diálogos.
El papel del guionista es muy importante, pues su trabajo es la base de todo el proyecto, si el guion es bueno el director puede hacer una película excelente, pero si este es deficiente aunque el director tenga muchos recursos, la película quedará vacía.
Sonido: En rodaje, los encargados del sonido cinematográfico son el técnico de sonido y los microfonistas. En la postproducción se suman el editor de sonido, el compositor de la música incidental y los artistas de efectos sonoros (foley) y de doblaje, para generar la banda sonora original. El sonido es parte fundamental del cine ya que la percepción del sonido en el cine incluye: vibraciones interpretada por el cerebro a través del sistema auditivo (procedencia, intensidad, tonalidad, materiales, espacio etc.), cualidades del sonido estéticas como texturas y frecuencias, y cualidades del sonido psicológicas (sugerentes, agradables, inquietantes o molestas). También se manejan estímulos sonoros. El sonido es muy importante porque amplía los límites de la pantalla, soluciona problemas narrativos, cohesiona el montaje, influye en el espectador de forma inconsciente y transmite historias y emociones.
Fotografía: El director de fotografía es la persona que determina cómo se va a ver la película, es decir, es quien determina, en función de las exigencias del director y de la historia, los aspectos visuales de la película: el encuadre, la iluminación, la óptica a utilizar etc. Es el responsable de toda la parte visual de la película, también desde el punto de vista conceptual, determinando la tonalidad general de la imagen y la atmósfera óptica de la película.
El equipo de fotografía es el más numeroso y se compone, además del director de fotografía, del camarógrafo, el primer asistente de cámara o foquista, el segundo asistente de cámara, el cargador de negativos, el gaffer o jefe de eléctricos, los eléctricos u operadores de luces, los grip u operadores de travelling o dolly, los estabilizadores de cámara (steady cam) y otros asistentes o aprendices.
Montaje: El montaje cinematográfico es la técnica de ensamblaje de las sucesivas tomas registradas en la película fotográfica para modelarlas en su forma narrativa, dramatúrgica y, específicamente, rítmica con el fin de construir frases audiovisuales: escenas y secuencias. Consiste en escoger (una vez que se ha rodado la película), ordenar y unir una selección de los planos registrados, según una idea y una dinámica determinada, a partir del guion, la idea del director y el aporte del montador. El montador sincroniza la imagen con el sonido (tarea habitualmente encomendada al ayudante de montaje). Visiona las tomas diarias junto al director y los miembros clave del equipo (el director de fotografía, que así supervisa su propio trabajo).
Hoy en día, muchas películas se montan en vídeo, y después ese montaje sirve de referencia para cortar y empalmar el negativo, que en sus inicios su base era de celuloide, y que posteriormente fue sustituido por acetato y poliéster, dada la alta peligrosidad del primero. La preparación de estas tomas diarias se desarrolla cada día a lo largo del rodaje de la película. La posproducción es el momento en que el montador ha reunido todo el material necesario para completar un primer montaje de la película. Después de que el director y el productor aprueban el montaje final, un montador de sonido especializado corrige los posibles problemas con este. Si fuera necesario, el montador de sonido regraba los diálogos en un estudio de grabación, mientras los actores ven en proyección la imagen correspondiente. Este proceso se conoce como doblaje. Los montadores de sonido reúnen las grabaciones y crean a veces nuevos sonidos (efectos sonoros) para intensificar la fuerza dramática de una escena. Mientras se prepara la banda de sonido, el montador también supervisa los efectos ópticos y los títulos que se van a incorporar a la película. Uno de los pasos finales es la preparación y la mezcla de las diferentes bandas sonoras en un único máster, primero magnético, que contendrá los diálogos, música, sonido directo y efectos de sonido, sincronizados con la imagen y adecuado al volumen de cada banda. La mezcla sin los diálogos hace posible el doblaje para la distribución de la película en otros idiomas.
Operador de cámara: Es el encargado de realizar y llevar a cabo todos los movimientos de cámara que sean necesarios para adaptarse al guion bajo la dirección del director.
Arte (Diseño de producción): El área artística puede tener un director de arte o varios, de ser necesario. En el caso de haber más de uno, estos están coordinados por un diseñador de producción, quien está a cargo de la estética general de la película. Estos directores tendrán asistentes y encargados específicos, como escenógrafos, encargados de vestuario, modistas, maquilladores, peluqueros/as, utileros y otros miembros suplementarios como pintores, carpinteros o constructores. También dependen de esta área especialistas en los efectos visuales y ópticos que se realicen en el rodaje, así como otros efectos realizados durante la fase de postproducción.
Stunts: Doble es la persona encargada de salvaguardar la integridad del actor que no cuenta con las habilidades necesarias para realizar escenas de riesgo. Estos están preparados física y mentalmente, son personas capaces y acostumbradas para hacer actividades de riesgo al rodar escenas en cine.
Storyboards: El storyboard es un guion gráfico que se utiliza para definir las secuencias, así como las variaciones de plano, gestos y posiciones de los actores, en cada una de las escenas antes de rodarla; en él vemos como si de un cómic se tratase la película completa. Además este elemento es fundamental para la buena comprensión del equipo técnico hacia lo que se va a rodar, incluyendo anotaciones con las dificultades de algunos planos o cosas a tener en cuenta. En la creación de un storyboard, los personajes y el fondo se pueden retratar únicamente mediante siluetas, pero siempre recalcando los elementos importantes en la acción como pueden ser flechas para indicar movimiento de cámara o de actores, o la expresión de un actor en un plano determinado para cuidar hasta el más mínimo detalle y la producción sea excelente.
Distribución y exhibición: Los distribuidores, generalmente empresas independientes de las productoras, compran los derechos de exhibición en salas de cine, o para su emisión por televisión, y venden los derechos de la película a los exhibidores (individuales o cadenas de exhibidores), cadenas de televisión, videoclubes u otros establecimientos donde se vendan las cintas de vídeo. Son también encargados de la publicidad y de la promoción de las películas, de hacer las copias necesarias para la exhibición y de controlar las cifras de ingresos y gastos. El productor cede al distribuidor un porcentaje de los ingresos de la película que por lo común alcanza el 50%. Además el distribuidor deduce de los beneficios del productor el importe de las copias de la película. Los mercados secundarios son aquellos que proporcionan ingresos adicionales, que no eran el objetivo inicial de la producción. Estos mercados incluyen una diversidad de objetos: juguetes con el nombre de los personajes de la película (especialmente en el caso de las de dibujos animados), camisetas, publicación del guion, cortometrajes sobre las incidencias del rodaje (el cómo se hizo o making of) y grabaciones en disco, casete o compacto de la banda sonora original. Los productores buscarán compositores conocidos a los que ceden los derechos de la distribución fonográfica de su música.
Géneros cinematográficos
En la teoría cinematográfica, los géneros son una forma de clasificar a las películas en grupos. Cada género está formado por películas que comparten ciertas similitudes, ya sea en su estilo, su temática, su intencionalidad, su forma de producción o el público al que van dirigidas.
Atendiendo a su forma de producción y su intencionalidad, cabe distinguir géneros como los siguientes:
Cine comercial: Son las películas creadas por la industria cinematográfica orientadas al gran público y con la generación de beneficios económicos como objetivo principal. A esta categoría pertenecen la mayoría de las películas que se proyectan en las salas de cine, y algunas de ellas son promocionadas mediante grandes campañas de publicidad.
Cine independiente: Una película independiente es una película de bajo presupuesto y hecha por pequeñas productoras. Una película independiente no es realizada por los grandes estudios.
Cine de animación: El cine de animación es aquel en el que se usan mayoritariamente técnicas de animación. El cine de imagen real registra imágenes reales en movimiento continuo, descomponiéndolo en un número discreto de imágenes por segundo. En el cine de animación no existe movimiento real que registrar, sino que se producen las imágenes individualmente y una por una (mediante dibujos, modelos, objetos y otras múltiples técnicas, como el Stop Motion), de forma tal que al proyectarse consecutivamente se produzca la ilusión de movimiento. Es decir, que mientras en el cine de imagen real se analiza y descompone un movimiento real, en el cine de animación se construye un movimiento inexistente en la realidad.
Cine documental: El cine documental es el que basa su trabajo en imágenes tomadas de la realidad. Generalmente se confunde documental con reportaje, siendo el primero eminentemente un género cinematográfico, muy ligado a los orígenes del cine, y el segundo un género televisivo.
Docuficción, híbrido entre el documental y la ficción, es un género practicado desde el primer documental, que se renueva desde finales de los años cincuenta.
Cine experimental: El cine experimental es aquel que utiliza un medio de expresión más artístico, olvidándose del lenguaje audiovisual clásico, rompiendo las barreras del cine narrativo estrictamente estructurado y utilizando los recursos para expresar y sugerir emociones, experiencias, sentimientos, utilizando efectos plásticos o rítmicos, ligados al tratamiento de la imagen o el sonido.
Cine de autor: El concepto de cine de autor fue acuñado por los críticos de los Cahiers du Cinéma para referirse a un cierto cine en el que el director tiene un papel preponderante en la toma de todas las decisiones, y en donde toda la puesta en escena obedece a sus intenciones. Suele llamarse de esta manera a las películas realizadas basándose en un guion propio y al margen de las presiones y limitaciones que implica el cine de los grandes estudios comerciales, lo cual le permite una mayor libertad a la hora de plasmar sus sentimientos e inquietudes en la película. Sin embargo, grandes directores de la industria, como Alfred Hitchcock, también pueden ser considerados «autores» de sus películas. Se define de acuerdo con su ámbito de aplicación y recepción, ya que no suele tratarse de un cine ligado a la industria, y no se dirige a un público amplio sino específico, y comparte a priori un interés por productos que se hallan fuera de los cánones clásicos. Un subgénero importante podría ser el cine abstracto.
Cine ambiental: El cine no solamente ha puesto en contacto al hombre con la naturaleza en diversos casos, sino que además ha sido, y sigue siendo en ocasiones, militante activo en la lucha por la defensa del medio ambiente. Además, el cine ha sido desde su nacimiento, el más fuerte medio de transmisión de conocimientos y de culturas, aportando a los espectadores infinitas posibilidades de encuentro con paisajes, naturaleza, lugares y costumbres.
Teoría del cine
La teoría del cine se basa en el principio de secuencias de fotografías continuas, es decir el cine trata de representar la fotografía en una secuencia continua para mostrar movimiento sin interrupciones.
El cine clásico tiene un estilo que enfatiza la continuidad y comprensibilidad de la película. Normalmente tiene caracteres fuertes, constantes durante toda la película y un argumento con un final feliz. El cine moderno no enfatiza estas características, al contrario, rechaza el cine clásico y su estilo; e intenta romper todo ese estilo y todas las convenciones de este. Directores diferentes utilizan montos variantes del estilo moderno.
Formatos cinematográficos
Alegoría del cine, con un proyector encendido. Vidriera policromada, modernista, del cine Ideal (Madrid).
El cine nació en el siglo XIX como consecución de una larga cadena de inventos y descubrimientos en torno a la fotografía. El hechizo que causaba la proyección de sombras chinescas o dibujos de lejanos países mediante lámparas mágicas se unió a los avances de la fotografía. Como fenómeno de masas, podemos hablar del nacimiento del cine con los hermanos Lumière. Pero no hay que olvidar que estos lo que hicieron fue perfeccionar el kinetoscopio de Thomas Alva Edison. Y que hubo muchos otros inventos que giraron en torno a cómo captar el movimiento.
Fue Thomas Alva Edison el creador, además, del formato cinematográfico por excelencia, el 35 mm, sobre un soporte de nitrato de celulosa. Este formato y los de ancho superior devinieron los de uso profesional, aunque hubo otros muchos empleados por cineastas o por la propia televisión:16 mm, 9,5 mm, Súper 8, etc.
El formato de pantalla ancha aparece en Hollywood a fines de la década de 1920, en diversos cortos e informativos para cine. Su estreno coincide con el boom de las películas en 3 dimensiones y la utilización de lentes estereoscópicas de colores rojo y azul (anaglifo), estrenadas en 1915.
Durante la Gran Depresión de la década de 1930 los estudios se vieron obligados a utilizar formatos de pantalla ancha de menor amplitud para bajar sus costos, pero fue hasta comienzos de los años 50, ante la arrolladora irrupción de la televisión, que los estudios volvieron a utilizar relaciones de aspecto mayores. En 1953, la cadena FOX lanzó uno de los procesos de creación de formato de pantalla ancha más populares entre los años 1953 y 1967: el Cinemascope, el antecesor del sistema que hoy conocemos por Panavisión, el más utilizado hoy en día. El legado que sobrevive hasta nuestros días es la pantalla ancha o panorámica.
Física/Cinemática
-
Física/Cinemática
< FísicaLa cinemática es una rama de la física dedicada al estudio del movimiento de los cuerpos en el espacio, sin atender a las causas que lo producen (lo que llamamos fuerzas). Por tanto la cinemática sólo estudia el movimiento en sí, a diferencia de la dinámica que estudia las interacciones que lo producen. El Análisis Vectorial es la herramienta matemática más adecuada para ellos.
En cinemática distinguimos las siguientes partes:La magnitud vectorial de la cinemática fundamental es el "desplazamiento" Δs, que experimenta un cuerpo durante un lapso Δt. Como el desplazamiento es un vector, por consiguiente, sigue la ley del paralelogramo, o la ley de suma vectorial. Asi si un cuerpo realiza un desplazamiento "consecutivo" o "al mismo tiempo" dos desplazamientos 'a' y 'b', nos da un deslazamiento igual a la suma vectorial de 'a'+'b' como un solo desplazamiento.

Observación sobre la notación: en el texto y en la ilustración se nombra a los vectores con letras negrillas y cursivas. En las fórmulas y ecuaciones, que se escriben con TeX, son vectores los que tienen una flecha sobre sus letras
Conceptos....
Modelo físico: Para estudiar la realidad, los físicos se sirven de 'modelos' que, con cierta aproximación y en determinadas condiciones, corresponden con ella. Se usan para realizar cálculos teóricos. Así, puede modelizarse un balón con una esfera para, por ejemplo, calcular su volumen con cierta aproximación conociendo su radio aproximado, aunque no es exactos.
Punto: Es un modelo físico. Se refiere a un elemento de volumen despreciable (se considerará sin volumen) situado en el espacio (en 3D. Busca 'espacio euclidiano' para más detalles).
Posición: Llamamos posición de un punto a su localización con respecto a un sistema de referencia (lo que en física se llama 'observador').
Sistema de referencia: Es aquel sistema coordenado con respecto al cual se da la posición de los puntos y el tiempo (a determinadas velocidades el tiempo cambia, buscad la paradoja de los gemelos). Profundizaremos más en este tema cuando se aborde el de Movimiento relativo.
Tiempo: Por nuestro lenguaje parece complicado de definir. Los griegos dieron una solución que, por ahora, nos puede valer. Llamamos tiempo al contínuo transcurrido entre dos instantes.
Partícula puntual: Es un modelo físico. Se refiere a un elemento de tamaño diferencial (muy pequeño) y masa concentrada en su posición.
Sólido rígido o, simplemente, sólido: Es otro modelo físico. Puede definirse de varias formas. La más usada es la que lo hace como un cuerpo cuyas distancias entre partículas permanecen constantes con el tiempo. Aunque ésto no ocurre en la realidad, para esfuerzos moderados una mesa seguira siendo rígida, pero un globo puede no responder a éste modelo.
Rapidez y aceleración
Diariamente escuchamos los conceptos de rapidez y aceleración como velocidad y aceleración solamente. Pero en física la velocidad y la aceleración son vectores, por lo que es claro y necesario su diferenciación y entendimiento. De aquí en adelante (más por costumbre que por ganas) llamaremos tanto a la rapidez y a la aceleración solamente como velocidad y aceleración (a menos que se especifique lo contrario).
Si cubre una masa puntual en un punto P en un tiempo Δt el tramo Δs, se llamara al cociente Δs / Δt su velocidad media vm en el intervalo de tiempo Δt o en el tramo Δs.
{\displaystyle v_{m}={\frac {\Delta s}{\Delta t}}}
Se observa que Δs aquí no es el desplazamiento, sino la longitud de arco: es el camino recorrido.La llamamos velocidad media porque la masa puntual no se mueve por el trayecto uniforme trazado. O sea estamos tomando sólo los puntos final e inicial para hacer los cálculos.
Hagamos el trayecto como Δs (de manera diferencial, o sea infinitesimal), al igual que al intervalo de tiempo Δt. Para Δs cercano a cero (o Δt cercano a cero, que tienda a cero) el cociente Δs/Δt como valor al límite, nos da la velocidad v de la masa puntual en el punto P, así:
{\displaystyle v=\lim _{\Delta s\to 0}{\frac {\Delta s}{\Delta t}}\equiv \lim _{\Delta t\to 0}{\frac {\Delta s}{\Delta t}}.} En el análisis se puede calcular ese valor al límite también como ds/dt. Así:{\displaystyle v={\frac {\operatorname {d} s}{\operatorname {d} t}}\,.} Tomemos luego una masa puntual que tiene en el punto P y en el tiempo t la velocidad v; y en el tiempo t + Δt y la velocidad v + Δv. Podemos calcular el cociente Δv/Δt como la aceleración media am de la masa puntual en el intervalo de tiempo Δt:{\displaystyle a_{m}={\frac {\Delta v}{\Delta t}}.} Para Δt cercano a cero se aspira a que ese cociente tenga un valor límite, la aceleracion a de la masa puntual para el tiempo t.{\displaystyle a=\lim _{\Delta t\to 0}{\frac {\Delta v}{\Delta t}}.} Para ese valor límite, se puede simplificar:{\displaystyle a={\frac {\operatorname {d} v}{\operatorname {d} t}}.} Es el camino s descrito como una función analítica del tiempo t, así s=s(t), así es la función de velocidad v(t) la primera derivada de la función s(t) con respecto al tiempo, la función de aceleración a(t) es la segunda derivada. La derivación con respecto al tiempo se puede también escribir como un punto sobre las variables.{\displaystyle v(t)={\frac {\operatorname {d} s(t)}{\operatorname {d} t}}={\dot {s}}(t);\quad \quad a(t)={\frac {\operatorname {d} v(t)}{\operatorname {d} t}}={\dot {v}}(t)={\frac {\operatorname {d} ^{2}s}{\operatorname {d} t^{2}}}\equiv {\ddot {s}}(t).} En sentido contrario se puede encontrar la función de velocidad y la función de la trayectoria a través de la integración:{\displaystyle v(t)=\int {a(t)\,\operatorname {d} t;\quad s(t)=\int {v(t)\,\operatorname {d} t=\iint {a(t)\,\operatorname {d} t\,\operatorname {d} t.}}}} En las integrales indefinidas de debe aumentar una constante que puede ser conocida con las condiciones iniciales del problema.Ejemplo: En caida libre una masa puntual se encuentra con una aceleración constante g. Esto es, cuando el tiempo t=0 verticalmente de arriba hacia abajo, tiene la velocidad v0 y sus coordenadas s0:
{\displaystyle v(t)=g\int {\operatorname {d} t=gt+v_{0};\quad s(t)=\int {\left({gt+v_{0}}\right)}}\operatorname {d} t={\frac {g}{2}}t^{2}+v_{0}t+s_{0}.} Velocidad y aceleración vectorial
Velocidad
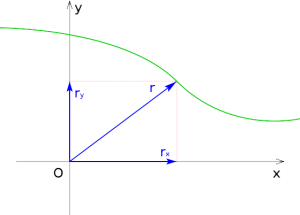
Vamos a ver ahora a una partícula, que atraviesa un espacio en una curva. Para el tiempo t se halla en P, para el tiempo t + Δt en Q. El lugar del punto esta descrito por su vector posición 'r'. Esta es una función de t y esta descrita por una función vectorial 'r'(t).
Asi:
{\displaystyle {\overrightarrow {r}}(t)=x\,{\overrightarrow {i}}+y\,{\overrightarrow {j}}+z{\overrightarrow {k}}}
y{\displaystyle {\overrightarrow {r}}(t+\Delta t)=\left({x+\Delta x}\right){\overrightarrow {i}}+\left({y+\Delta y}\right){\overrightarrow {j}}+\left({z+\Delta z}\right){\overrightarrow {k}}\,,}
donde i, j y k son los vectores unitarios de los ejes de cordenadas.El desplazamiento de la partícula en un determinado intervalo de tiempo es:
{\displaystyle \Delta {\overrightarrow {r}}={\overrightarrow {r}}\left({t+\Delta t}\right)-{\overrightarrow {r}}\left(t\right)=\Delta x\,{\overrightarrow {i}}+\Delta y\,{\overrightarrow {j}}+\Delta z\,{\overrightarrow {k}}\,.}
El cociente Δr/Δt es la velocidad media (vectorial) vm de la partícula en el intervalo de tiempo Δt. Es{\displaystyle {\frac {\Delta {\overrightarrow {r}}}{\Delta t}}={\frac {\Delta x}{\Delta t}}{\overrightarrow {i}}+{\frac {\Delta y}{\Delta t}}{\overrightarrow {j}}+{\frac {\Delta z}{\Delta t}}{\overrightarrow {k}}\,.}
Aqui es (mirar arriba: rapidez y aceleración) Δx/Δt la rapidez media de la partícula paralela al eje X, Δy/Δt la rapidez media paralela al eje Y y Δz/Δt la rapidez media paralela al eje Z en un intervalo Δt.El vector resultante, del cociente Δr/Δt para Δt cercano a cero, se llama velocidad vP = v'(t) de la particula en P o en el tiempo t.
{\displaystyle {\overrightarrow {v}}_{P}={\overrightarrow {v}}(t)=\lim _{\Delta t\to 0}{\frac {\Delta {\overrightarrow {r}}}{\Delta t}}={\frac {\operatorname {d} {\overrightarrow {r}}}{\operatorname {d} t}}={\frac {\operatorname {d} x}{\operatorname {d} t}}{\overrightarrow {i}}+{\frac {\operatorname {d} y}{\operatorname {d} t}}{\overrightarrow {j}}+{\frac {\operatorname {d} z}{\operatorname {d} t}}{\overrightarrow {k}}\,.}
La función vectorial v'(t) es la primera derivada de la función de posición r(t) en el tiempo.{\displaystyle {\overrightarrow {v}}(t)={\frac {\operatorname {d} {\overrightarrow {r}}}{\operatorname {d} t}}={\dot {\vec {r}}}}
Como se ve, son las componentes escalares del vector v(t) identicos con la velocidad instantanea paralela a los ejes:{\displaystyle v_{x}={\frac {\operatorname {d} x}{\operatorname {d} t}},\quad v_{y}={\frac {\operatorname {d} y}{\operatorname {d} t}},\quad v_{z}={\frac {\operatorname {d} z}{\operatorname {d} t}}\,.}
El recta en el punto P en la direccion del vector vP se llama La Tangente a la curva en PAceleración
Análogamente vamos ahora a definir la función vectorial de la aceleración:
{\displaystyle {\overrightarrow {a}}(t)=\lim _{\Delta t\to 0}{\frac {\Delta {\overrightarrow {v}}}{\Delta t}}={\frac {\operatorname {d} {\overrightarrow {v}}}{\operatorname {d} t}}={\dot {\vec {v}}}={\ddot {\vec {r}}}\,.}
La función vectorial de la aceleración proviene de las componentes escalares de la función velocidad y de la función posición, así:{\displaystyle {\overrightarrow {a}}(t)={\frac {\operatorname {d} }{\operatorname {d} t}}\left({v_{x}{\overrightarrow {i}}+v_{y}{\overrightarrow {j}}+v_{z}{\overrightarrow {k}}}\right)={\frac {\operatorname {d} v_{x}}{\operatorname {d} t}}{\overrightarrow {i}}+{\frac {\operatorname {d} v_{y}}{\operatorname {d} t}}{\overrightarrow {j}}+{\frac {\operatorname {d} v_{z}}{\operatorname {d} t}}{\overrightarrow {k}}\,,} {\displaystyle {\overrightarrow {a}}(t)={\frac {\operatorname {d} ^{2}x}{\operatorname {d} t^{2}}}{\overrightarrow {i}}+{\frac {\operatorname {d} ^{2}y}{\operatorname {d} t^{2}}}{\overrightarrow {j}}+{\frac {\operatorname {d} ^{2}z}{\operatorname {d} t^{2}}}{\overrightarrow {k\,.}}}
Como se conoce, son las componentes escalares del vector velocidad igual a la dirección de la velocidad instantánea en los ejes de coordenadas.En sentido contrario se puede hallar por integración las correspondientes funciones.
Ejemplo: Para la caída libre con velocidad inicial v0 de un punto con el vector posición r0 (vertical o lanzamiento curvo).Cuando el eje Z (vector unitario k) esta dirigido verticalmente hacia abajo, es
{\displaystyle {\overrightarrow {a}}=-g{\overrightarrow {k}}\,,\quad {\overrightarrow {v}}=-\int {g{\overrightarrow {k}}\,\operatorname {d} t=-g\,t}{\overrightarrow {k}}+{\overrightarrow {v}}_{0},} {\displaystyle {\overrightarrow {r}}=\int {\left({-g\,t{\overrightarrow {k}}+{\overrightarrow {v}}_{0}}\right)\operatorname {d} t=-{\frac {g}{2}}t^{2}{\overrightarrow {k}}+{\overrightarrow {v}}_{0}\,t}+{\overrightarrow {r}}_{0\,.}} Mientras el vector velocidad siempre tiene dirección tangencial, puede estar dirigido opcionalmente el vector aceleración. En un análisis profundo, la aceleración se descompone en dos componentes, en la una dirección es tangencial (aceleración tangencial) y la otra esta en dirección vertical (aceleración normal).La aceleración tangencial cambia solo el valor de la velocidad (esta es la rapidez)
Para esta descomposición de los vectores de la aceleración introducimos la curva s, este es el largo de la trayectoria, que recorre la partícula en la curva. Este arco cuenta con un punto cero escogido, que de todas formas aquí no juega ningún papel, aquí solo necesitamos el diferencial ds del arco. Además introducimos el vector unitario tangencial t y hacemos uso de la geometría diferencial. El vector unitario tangente t es el vector
{\displaystyle {\overrightarrow {t}}={\frac {\overrightarrow {v}}{v}}\,,}
así denominado, es igual al vector v dividido para su módulo v. Este módulo es igual a la rapidez y es otra vez el desplazamiento sobre la curva sobre el tiempo. Asi es:{\displaystyle {\overrightarrow {v}}=v\,{\overrightarrow {t}}={\frac {\operatorname {d} s}{\operatorname {d} t}}{\overrightarrow {t}}\,.}
Si diferenciamos para el tiempo tenemos que{\displaystyle {\overrightarrow {a}}={\frac {\operatorname {d} ^{2}s}{\operatorname {d} t^{2}}}{\overrightarrow {t}}+{\frac {\operatorname {d} s}{\operatorname {d} t}}{\frac {\operatorname {d} {\overrightarrow {t}}}{\operatorname {d} t}}={\frac {\operatorname {d} ^{2}s}{\operatorname {d} t^{2}}}{\overrightarrow {t}}+{\frac {\operatorname {d} s}{\operatorname {d} t}}{\frac {\operatorname {d} {\overrightarrow {t}}}{\operatorname {d} s}}{\frac {\operatorname {d} s}{\operatorname {d} t}}={\frac {\operatorname {d} ^{2}s}{\operatorname {d} t^{2}}}{\overrightarrow {t}}+v^{2}{\frac {\operatorname {d} {\overrightarrow {t}}}{\operatorname {d} s}}\,.} Aqui la longitud del vector unitario tangencial t es constante (cercano a 1), esta el vector desplazamiento dt/ds - cuando no es igual a cero - verticalmente hacia t.
De la geometría diferencial tenemos, que el vector desplazamiento dt/ds- tiene la dirección del vector unitario normal n y
- el valor k = 1/ρ
De aquí es k la curvatura de la curva en el punto observado y ρ su radio de curvatura. El vector unitario normal n es dirigido hacia (momentaneamente) un punto medio de la curvatura (hacia dentro).
Siguiendo esto{\displaystyle {\frac {\operatorname {d} {\overrightarrow {t}}}{\operatorname {d} s}}=k{\overrightarrow {n}}={\frac {1}{\rho }}{\overrightarrow {n}}\,.}
Con esto nos da como resultado{\displaystyle {\overrightarrow {a}}={\frac {\operatorname {d} ^{2}s}{\operatorname {d} t^{2}}}{\overrightarrow {t}}+{\frac {v^{2}}{\rho }}{\overrightarrow {n}}\,.}
El vector a esta entre t y n' dirigido, en el plano de la curva en un determinado punto.El modulo de la aceleración tangencial es - como se esperaba:
{\displaystyle a_{tan}={\frac {\operatorname {d} ^{2}s}{\operatorname {d} t^{2}}}={\frac {\operatorname {d} v}{\operatorname {d} t}}\,,}
el modulo de la aceleración normal es{\displaystyle a_{nor}={\frac {v^{2}}{\rho }}.}
Este par de ecuaciones tienen su interpretación: La aceleración de una partícula da lugar a la aparición de una fuerza. La dirección de esa fuerza determina la dirección de la aceleración. La componente tangencial de la aceleración causa un cambio en la velocidad, la componente normal de la aceleración causa la curvatura de la curva. El radio de curvatura de la curva en un determinado punto resulta de la aceleración normal y de la velocidad así:{\displaystyle \rho ={\frac {v^{2}}{a_{nor}}}.} Movimiento circular
Una particula P se mueve en una circunferencia. Colocamos un eje de coordenadas XY y en el origen O del sistema de coordenadas en el centro de la circunferencia.
Entonces es- {\displaystyle {\overrightarrow {r}}=x_{r}{\overrightarrow {i}}+y_{r}{\overrightarrow {j}}=\left({r\cos \varphi }\right)\,{\overrightarrow {i}}+\left({r\sin \varphi }\right){\overrightarrow {j}}\,.}
Analogo a la velocidad y a la aceleracion podemos definir la velocidad angular ω así
- {\displaystyle \omega =\lim _{\Delta t\to 0}{\frac {\Delta \varphi }{\Delta t}}={\frac {\operatorname {d} \varphi }{\operatorname {d} t}}\,,}
y a la aceleracion angular α
- {\displaystyle \alpha =\lim _{\Delta t\to 0}{\frac {\Delta \omega }{\Delta t}}={\frac {\operatorname {d} \omega }{\operatorname {d} t}}={\frac {\operatorname {d} ^{2}\varphi }{\operatorname {d} t^{2}}}\,.}
Cuando t = 0 es también φ = 0, entonces es
- {\displaystyle \varphi \left(t\right)=\int _{0}^{t}{\omega \,\operatorname {d} t}=\int _{0}^{t}{\left[{\int _{0}^{t}{\alpha \,\operatorname {d} t}}\right]}\operatorname {d} t\,.}
Movimiento circular uniforme
Un movimiento circular con velocidad angular constante se lo llama uniforme. Entonces
- {\displaystyle \varphi (t)=\varphi (0)+\omega t\quad y\;\,para\quad \varphi (0)=0\quad \Rightarrow \quad \varphi (t)=\omega \,t.}
La ecuacion del vector posición es
- {\displaystyle {\overrightarrow {r}}=r\left({\cos \omega \,t}\right){\overrightarrow {i}}+r\left({\sin \omega \,t}\right){\overrightarrow {j}}\,.}
Con esto nos da la velocidad
- {\displaystyle {\overrightarrow {v}}={\frac {\operatorname {d} {\overrightarrow {r}}}{\operatorname {d} t}}=-r\omega \left({\sin \omega \,t}\right){\overrightarrow {i}}+r\omega \left({\cos \omega \,t}\right){\overrightarrow {j}}}
y
- {\displaystyle v={\sqrt {v_{x}^{2}+v_{y}^{2}}}=r\omega {\sqrt {\sin ^{2}\omega t+\cos ^{2}\omega t}}=r\omega \,.}
Efectuando el producto escalar entre los vectores r y v obtenemos:
- {\displaystyle {\begin{aligned}{\overrightarrow {r}}\,\cdot {\overrightarrow {v}}&=r\left({\cos \omega \,t}\right)\left[-r\omega \left({\sin \omega \,t}\right)\right]+r\left({\sin \omega \,t}\right)r\omega \left({\cos \omega \,t}\right)\\&=-r^{2}\omega \left({\sin \omega \,t}\right)\left({\cos \omega \,t}\right)+r^{2}\omega \left({\sin \omega \,t}\right)\left({\cos \omega \,t}\right)\\&=0\end{aligned}}}
Con lo cual resulta que los vectores r y v son perpendiculares. Para la aceleracion tenemos que
- {\displaystyle {\overrightarrow {a}}={\frac {\operatorname {d} {\overrightarrow {v}}}{\operatorname {d} t}}=-\,r\omega ^{2}\left({\cos \omega \,t}\right){\overrightarrow {i}}-r\omega ^{2}\left({\sin \omega \,t}\right){\overrightarrow {j}}}
y así
- {\displaystyle {\overrightarrow {a}}=-\,\omega ^{2}{\overrightarrow {r}}\quad \Rightarrow \quad a=\omega ^{2}r={\frac {v^{2}}{r}}\,.}
La aceleracion esta dirigida hacia O (aceleracion centripeta), y su modulo es constante.
Movimiento circular uniformemente acelerado
Aqui la aceleracion angular α es constante y también ω(0) = 0
- {\displaystyle \omega \left(t\right)=\alpha \,t=\left({\frac {\operatorname {d} \varphi }{\operatorname {d} t}}\right)_{t}.}
También, cuando φ(0)=0, así para el angulo de rotacion
- {\displaystyle \varphi \left(t\right)=\int _{0}^{t}{\omega \,\operatorname {d} t}=\int _{0}^{t}{\alpha \,t}\,\operatorname {d} t={\frac {\alpha }{2}}t^{2}.}
Asi tenemos también que
- {\displaystyle {\overrightarrow {r}}=r\left({\cos {\frac {\alpha }{2}}\,t^{2}}\right){\overrightarrow {i}}+r\left({\sin {\frac {\alpha }{2}}\,t^{2}}\right){\overrightarrow {j}}\,}
- {\displaystyle {\overrightarrow {v}}={\frac {\operatorname {d} {\overrightarrow {r}}}{\operatorname {d} t}}=r\alpha \,t\left[{-\left({\sin \,{\frac {\alpha }{2}}t^{2}}\right){\overrightarrow {i}}+\left({\cos {\frac {\alpha }{2}}t^{2}}\right){\overrightarrow {j}}}\right]=r\omega \left[{-\left({\sin \,{\frac {\alpha }{2}}t^{2}}\right){\overrightarrow {i}}+\left({\cos {\frac {\alpha }{2}}t^{2}}\right){\overrightarrow {j}}}\right]}
y
- {\displaystyle {\overrightarrow {a}}={\frac {\operatorname {d} {\overrightarrow {v}}}{\operatorname {d} t}}=r\alpha \left[{-\left({\sin {\frac {\alpha }{2}}t^{2}}\right){\overrightarrow {i}}+\left({\cos {\frac {\alpha }{2}}t^{2}}\right){\overrightarrow {j}}}\right]+}
-
- {\displaystyle +\,r\alpha ^{2}t^{2}\left[{\left({-\cos {\frac {\alpha }{2}}t^{2}}\right){\overrightarrow {i}}-\left({\sin {\frac {\alpha }{2}}t^{2}}\right){\overrightarrow {j}}}\right].}
- {\displaystyle +\,r\alpha ^{2}t^{2}\left[{\left({-\cos {\frac {\alpha }{2}}t^{2}}\right){\overrightarrow {i}}-\left({\sin {\frac {\alpha }{2}}t^{2}}\right){\overrightarrow {j}}}\right].}
-
o
- {\displaystyle {\overrightarrow {a}}=\left[{-r\alpha \left({\sin \varphi }\right)-r\omega ^{2}\left({\cos \varphi }\right)}\right]{\overrightarrow {i}}+}
-
- {\displaystyle +\left[{r\alpha \left({\cos \varphi }\right)-r\omega ^{2}\left({\sin \varphi }\right)}\right]{\overrightarrow {j}}.}
- {\displaystyle +\left[{r\alpha \left({\cos \varphi }\right)-r\omega ^{2}\left({\sin \varphi }\right)}\right]{\overrightarrow {j}}.}
-
Asi, podemos dedecir que la componente radial de la aceleracion (y su direccion) es
- {\displaystyle \,a_{rad}=r\omega ^{2}}
y su componente tangencial es
- {\displaystyle \,a_{tan}=r\alpha }
La velocidad angular como medida de direccion
A veces es muy util ver a la velocidad angular como medida de la direccion y representarlo a traves de un en el eje de giro y su modulo sea igual a la velocidad angular. Asi se introduce un vector unitario a la medida ω e como el vector vector. O sea su falta lo esencial e indispensable propiedad de los vmysytrymrtectores: esta no puede sudos movimientos de rotacion (donde ambas partes de la velocidad deban ser investigadas particularmente) es util la introducción de unos vectores de rotacion.
Ecuaciones de Movimiento en un sistema de coordenadas polares
Velocidad en coordenadas Polares
La velocidad v de una partícula material puede descomponerse en distintos tipos de componentes. Es usual e importante que se descomponga en componentes que tengan la dirección de los ejes de coordenadas, así se obtiene en la forma siguiente:
{\displaystyle {\overrightarrow {v}}=v_{x}{\overrightarrow {i}}+v_{y}{\overrightarrow {j}}+v_{z}{\overrightarrow {k}}={\frac {\operatorname {d} x}{\operatorname {d} t}}{\overrightarrow {i}}+{\frac {\operatorname {d} y}{\operatorname {d} t}}{\overrightarrow {j}}+{\frac {\operatorname {d} z}{\operatorname {d} t}}{\overrightarrow {k}}.}

































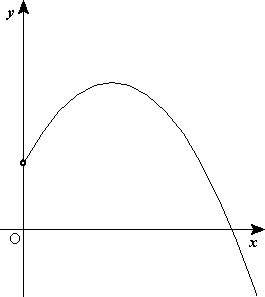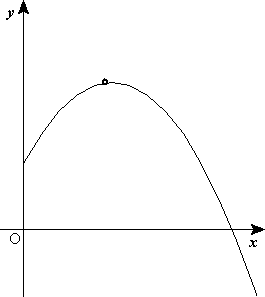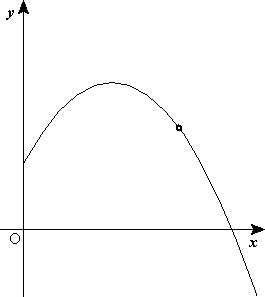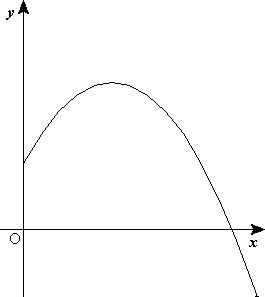
 que sigue una trayectoria parabólica.
que sigue una trayectoria parabólica.



























































![{\displaystyle \varphi \left(t\right)=\int _{0}^{t}{\omega \,\operatorname {d} t}=\int _{0}^{t}{\left[{\int _{0}^{t}{\alpha \,\operatorname {d} t}}\right]}\operatorname {d} t\,.}](https://wikimedia.org/api/rest_v1/media/math/render/svg/f88051e114316d650fb4fd419d2f83eac12c73e1)




![{\displaystyle {\begin{aligned}{\overrightarrow {r}}\,\cdot {\overrightarrow {v}}&=r\left({\cos \omega \,t}\right)\left[-r\omega \left({\sin \omega \,t}\right)\right]+r\left({\sin \omega \,t}\right)r\omega \left({\cos \omega \,t}\right)\\&=-r^{2}\omega \left({\sin \omega \,t}\right)\left({\cos \omega \,t}\right)+r^{2}\omega \left({\sin \omega \,t}\right)\left({\cos \omega \,t}\right)\\&=0\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/2452256307901ce1a7b53b4592a6da7b29915a0e)





![{\displaystyle {\overrightarrow {v}}={\frac {\operatorname {d} {\overrightarrow {r}}}{\operatorname {d} t}}=r\alpha \,t\left[{-\left({\sin \,{\frac {\alpha }{2}}t^{2}}\right){\overrightarrow {i}}+\left({\cos {\frac {\alpha }{2}}t^{2}}\right){\overrightarrow {j}}}\right]=r\omega \left[{-\left({\sin \,{\frac {\alpha }{2}}t^{2}}\right){\overrightarrow {i}}+\left({\cos {\frac {\alpha }{2}}t^{2}}\right){\overrightarrow {j}}}\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/610a2564823b8defefeeecbe611e585aca6af86a)
![{\displaystyle {\overrightarrow {a}}={\frac {\operatorname {d} {\overrightarrow {v}}}{\operatorname {d} t}}=r\alpha \left[{-\left({\sin {\frac {\alpha }{2}}t^{2}}\right){\overrightarrow {i}}+\left({\cos {\frac {\alpha }{2}}t^{2}}\right){\overrightarrow {j}}}\right]+}](https://wikimedia.org/api/rest_v1/media/math/render/svg/f27d7325d8770cf13ee8446c138f086d328e25d8)
![{\displaystyle +\,r\alpha ^{2}t^{2}\left[{\left({-\cos {\frac {\alpha }{2}}t^{2}}\right){\overrightarrow {i}}-\left({\sin {\frac {\alpha }{2}}t^{2}}\right){\overrightarrow {j}}}\right].}](https://wikimedia.org/api/rest_v1/media/math/render/svg/b85262543608f244520a74930287c29b567f7430)
![{\displaystyle {\overrightarrow {a}}=\left[{-r\alpha \left({\sin \varphi }\right)-r\omega ^{2}\left({\cos \varphi }\right)}\right]{\overrightarrow {i}}+}](https://wikimedia.org/api/rest_v1/media/math/render/svg/5796d2f39e4a3a173a01ac6885e4fd4703696c98)
![{\displaystyle +\left[{r\alpha \left({\cos \varphi }\right)-r\omega ^{2}\left({\sin \varphi }\right)}\right]{\overrightarrow {j}}.}](https://wikimedia.org/api/rest_v1/media/math/render/svg/f61d1f3b5ba7920a08d07a4d4628620cad7e77e3)